Reverse engineering the Amiga 600 keyboard
14 April 2014 - ~8 Minutes Hardware Hacking
Operation “turn an old Amiga 600 into a Raspberry Pi”
The Raspberry Pi is a great little idea, designed to bring “home computing” - and being able to program your home computer - to a new generation. Being small, cheap and hackable, it’s also caught the attention of a lot of people who actually did program their home computer when they were kids in the 80s and 90s - and has become quite common in “retro computing” projects. A quick Google will reveal many people hacking together Raspberry Pi systems into the cases of the Commodore 64s, Sinclair QLs and ZX81s that they used to know and love.
I’m a thirty-something who grew up in the home computer revolution of the 80s and 90s, and so therefore I’m part of this retro computing trend. This is my quest - and my chosen host, the Amiga 600, which, through a convoluted and uninteresting story, I happen to have a sample of in the garage.

The Amiga 600
You can see the Amiga 600 here (click the picture for the full-size version). It’s a neat little box, stylish in a certain way, with a decent size keyboard, some LEDs, a floppy drive, and plenty of outlets for I/O ports. Most importantly, absolutely loads of room for a Raspberry Pi (once the Amiga mainboard has been removed, of course.) I’d prefer an Amiga 1200, of course, however sometime in the 90s I towerised my A1200 and threw away the original case, so the A600 will have to do.
Opening up the case is fairly straightforward. This reveals that the keyboard and LEDs and clipped to the upper part of the case, and a pair of cables connect them to the mainboard - these cables need to be disconnected in order to completely remove the top part of the case. After that, removing a few more screws allows the floppy drive to be removed, and then the mainboard.
So, we’re interested in the top half of the case. There are two cables coming out from here - the first is for the LEDs. These are really simple - it’s just a four pin cable, one for ground, and one for each LED. The little circuit board already has resistors in series with the LEDs, so driving the LEDs is as simple as connecting the appropriate wire to a digital output pin on a Raspberry Pi or an Arduino. On the basis the Amiga PSUs supply only 12v and 5v power, I’m working on the assumption that the resistor and LED combination is correct for a 5v supply. An Arduino Micro works natively at 5V so it can drive these LEDs with no extra components required.
The keyboard is where things start to interesting. If you dismantle the keyboard by removing the large number of screws holding it together, you’ll find that behind the keys is this membrane:

Membrane inside the Amiga 600 keyboard
Each pair of pads in a diagonal pattern represents a key - when the key is pressed, a conductor on the back of the key closes the circuit between the two pads. You can trace the conductors up to the cable at the top of the image - this cable would normally be plugged into a connector on the A600 mainboard. So when a key is pressed, current is able to flow between two of the wires; by finding out which combinations of wires conduct, you can work out which keys are pressed.
The keyboard is arranged into “rows” and “columns”. Each key is connected to two pads; one will be for a row, the other for a column. By painstakingly examining all of the conductors in the membrane, I discovered that the keyboard is arranged as 6 rows and 22 columns. In addition to this, there is the Caps Lock LED, which requires a further two conductors, bringing the total up to 30 conductors on the cable that connects to the mainboard.
So my theory is that my driving some current down the “row” lines, one at a time, and then looking for a circuit on the “column” lines, I will be able to determine what keys are pressed. However, there’s a problem - that means I require 6 outputs and 22 inputs, or 28 GPIO pins - 29 if I also want to drive the Caps Lock LED. A Raspberry Pi doesn’t have this many GPIO pins, and neither does the aforementioned Arduino Micro - an Arduino Mega could do it, but that’s a bit on the large side for this project.
The device that can easily handle this is a GPIO extender - in this case, the Microchip MCP23017. This device provides 16 GPIO pins, so two of these together can handle all of the signals I require. They are controlled by I2C, a data bus that supports multiple devices, requires only two data lines, and is supported by both the Raspberry Pi and Arduino devices. And, it’s cheap - about £1 each.
The last significant piece is how to physically connect this keyboard to, well, anything except the A600 mainboard. The A600 mainboard has an unusual connector for the keyboard ribbon cable. The main problem I have as an inexperienced hardware hacker is knowing the right names for things - once I know the name then Google is easy to use, but until then I’m largely in the dark. These connectors are often referred to as Molex connectors, but Molex make a heck of a lot of connectors. Fortunately, I eventually discovered that this particular ribbon cable is called a Flat Conductor Cable, or FCC, or sometimes FPC or FFC, and the mainboard features a FCC “ZIF” (Zero Insertion Force) connector. That’s enough information to lead myself to this category on the RS Components website, and from there to this part: 30 way straight ZIF FFC connector,1.25mm.
The final piece is for the Caps Lock LED - unlike the power and drive LEDs, there’s no resistor on the keyboard LED, so I’ll need to supply one.
So I have my bill of materials - two MCP23017 GPIO extenders, a 30 way straight ZIF FFC connector, a resistor, and something with an I2C bus to drive the 23017s. There is however a small problem - the ZIF connector is not going to be easily wired up to a breadboard. So, rather than prototype out a solution using these devices, I’ve decided to take a chance and go straight for the custom PCB route. Here’s my design - once it’s back from Fritzing Fab, I’ll find out if I have designed it right, and write Part 2 of this project!
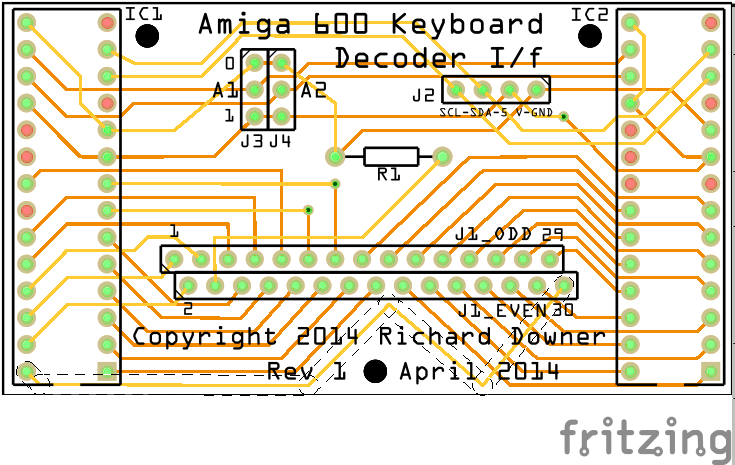
My custom PCB design for the Amiga 600 keyboard interface
UPDATE: the results
Apologies to those who have found this site and wondered what happened next. As with many home hobby projects, it never quite got finished, but here’s what did happen.
I did get the PCB back from Fritzing Fab, and it looked very smart. The components that I had identified were the correct ones, and assembly was mostly straightforward (one PCB ruined when I soldered the ZIF FCC connector back to front).
The “something with an I2C bus” was an Arduino Micro. It has a useful feature which is that it can behave as a USB HID (Human Interface Device) gadget. Combined with my PCB, I end up with something with a USB port that can be plugged into any computer and behave as a keyboard, without any special drivers or wiring.
In the end, I did get a good proof-of-concept: the software I wrote for the Arduino was incomplete and buggy, but it did work: you could type keys on the keyboard, and get the same character appearing on the computer screen.
There’s a couple of “unfortunately"s. The first is that I never got the software to a truly usable state. The second one is that in the intervening 4 years, I seem to have lost the source code.
If you’d like to have a shot at making your own keyboard interface, you can download the Fritzing files here: A600-keyboard-interface.fzz. This is licensed under the MIT License:
Copyright 2014 Richard Downer Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated documentation files (the “Software”), to deal in the Software without restriction, including without limitation the rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit persons to whom the Software is furnished to do so, subject to the following conditions:
The above copyright notice and this permission notice shall be included in all copies or substantial portions of the Software.
THE SOFTWARE IS PROVIDED “AS IS”, WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
And if the Arduino files show up, then I will make a further update here to share them with you.
However, if you don’t fancy doing all the hard work yourself, just buy a Keyrah from your favourite Amiga dealer (Google can help).
About the author
Richard Downer is a software engineer turned cloud solutions architect, specialising in AWS, and based in Scotland. Richard's interest in technology extends to retro computing and amateur hardware hacking with Raspberry Pi and FPGA.